Einmaleins (1x1) Klasse 2
Das kleine Einmaleins (1x1) spielerisch üben
Das kleine Einmaleins zu üben ist manchmal ziemlich mühselig. Es kann deshalb sinnvoll sein, den Übungsalltag mit einem Lernspiel aufzulockern.
Das braucht man für das Spiel:
- zwei Würfel
- ein kariertes Blatt
- zwei verschiedenfarbige Stifte
- einen Mitspieler
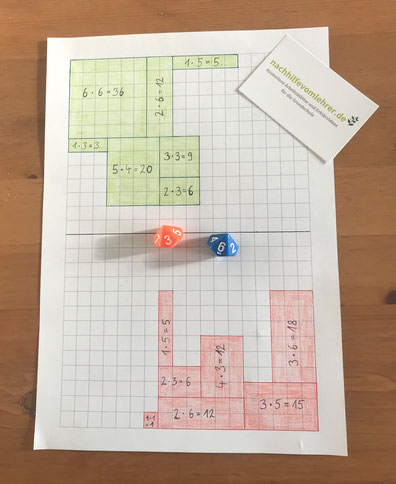
In der Mitte des Spielfeldes wird eine Linie gezogen. Diese Linie trennt das Spielfeld von Spieler 1 und das Spielfeld von Spieler 2. Nun würfelt jeder abwechselnd mit beiden Würfeln gleichzeitig. Die gewürfelten Zahlen ergeben eine Malaufgabe. Auf dem Bild zeigen die Würfel z.B. die Aufgabe 3 ∙ 6.
Nun muss im eigenen Spielfeld ein Rechteck gezeichnet werden, dass die Aufgabe darstellt (in diesem Fall: 3 Felder ∙ 6 Reihen = 18 Felder). In jedes Rechteck wird die Aufgabe mit Ergebnis geschrieben (wir wollen ja das kleine Einmaleins üben). Der Spieler, der beim Zeichnen als erstes die Linie in der Mitte übertreten muss, verliert.
Für Anfänger im kleinen Einmaleins empfiehlt es sich, zwei normale 6-seitige Würfel und Papier mit 1cm² großen
Kästchen* zu nehmen. Um wirklich das ganze Einmaleins zu üben, sollten später zwei 10-seitige Würfel und Papier mit 0,5cm² großen Kästchen benutzt werden. Wenn du keine 10-seitigen
Würfel hast, kannst du
hier günstig welche kaufen*. Würfel mit sechs Seiten findest du hier*.
Eine zweite Spielvariante besteht darin, möglichst viel Fläche des Blattes „einzunehmen“, bis man einen Wurf nicht mehr einzeichnen kann. Eine Grenzlinie wird hierfür nicht gezogen. Am Ende des
Spieles zählt jeder Spieler die Ergebnisse seiner Malaufgaben zusammen, um die Gesamtflächengröße auszurechnen.
So üben die Kinder nicht einfach nur Malaufgaben. Sie „sehen“ sie beim Zeichnen auch immer. Die Aufgabe 3 ∙ 6 bedeutet also 3 Reihen mit jeweils 6 Kästchen. Ganz nebenbei erwerben die Kinder noch
ein Verständnis über Flächeninhalte.
😊
Wer darüber hinaus Lust auf ein Kartenspiel zum Einmaleins hat, kann sich das Lernspiel SpielMal* anschauen. Es kann in zwei einfachen und in einer strategischen Variante gespielt werden und bietet eine angenehme Abwechslung zum Lernalltag.
Wichtig: Wie das Einmaleins gelernt werden sollte
Das Einmaleins sollte ein Kind bis zur Mitte der 3. Klasse auswendig können. Dabei ist es allerdings eine schlechte Idee, die Aufgaben Reihe um Reihe, wie ein Gedicht, auswendig zu lernen. Gerade lernschwachen Kindern wird es dadurch schwer bis unmöglich gemacht das Einmaleins zu verstehen.
Warum ist das so? Zum Einen verstehen viele Kinder nicht, was mathematisch hinter den Aufgaben steckt. Sie lernen die Malreihen wie ein Gedicht auswendig... ohne zu wissen, was es bedeutet. Was man nicht versteht, vergisst man auch schnell wieder. Dementsprechend wird das Auswendiglernen sehr mühselig.
Zum Anderen umfasst das Einmaleins (ohne die 0) insgesamt 100 Aufgaben. Wer also die Malreihen Reihe um Reihe auswendig lernt, muss 100 Fakten stur auswendig pauken. Das ist eine ganze Menge! Allerdings kann diese Anzahl erheblich reduziert werden!
Die Anzahl an Aufgaben wird reduziert, indem man die mathematischen Zusammenhänge der Malaufgaben nutzt:
- Malaufgaben können getauscht werden. Wer weiß, was 2 ∙ 7 ist, der weiß auch 7 ∙ 2... eine Einsicht, die durch das Auswendig lernen, Reihe um Reihe, eher erschwert wird. Das Tauschgesetz reduziert die zu lernenden Aufgaben von 100 auf nur noch 55 Aufgaben!
- Kernaufgaben sind Aufgaben, die sich die Kinder in der Regel leicht merken. Deswegen werden sie als erstes gelernt. Malaufgaben mit 10 sind kein Problem. Auch
Malaufgaben mit 2 sind nicht schwierig, weil Verdopplungsaufgaben (4+4, 7+7...) bereits vorher intensiv geübt wurden. Hier müssen Kinder nur noch lernen, dass 2 ∙ 7 das Gleiche ist wie 7 + 7... schon müssen wir nur noch 28 Aufgaben lernen!
-
Auch Malaufgaben mit 5 können leicht gelernt werden: 5 ∙ 4 ist die Hälfte von 10 ∙ 4... Nun sind wir nur noch bei 23
Aufgaben.
- Die restlichen 23 Aufgaben erleichtert man sich durch strategisches Vorgehen: 3 ∙ 7 kann von der Kernaufgabe 2 ∙ 7 abgeleitet werden (einfach einen 7er-Schritt weiter), für 9 ∙ 7 rechne ich erst 10 ∙ 7 und gehe dann einen Siebener-Schritt zurück. Das ist viel weniger fehleranfällig, als die ganze Reihe der 7 bis zu 9 ∙ 7 hochzurechnen!
Das Ziel ist dabei ganz klar, dass die Kinder das Einmaleins irgendwann schnell und sicher beherrschen! Damit das effizient und nachhaltig geschieht, müssen Grundvorstellungen
aufgebaut und Zusammenhänge genutzt werden. Um es noch einmal zu betonen: Gerade rechenschwache Kinder profitieren davon! Leistungsstarke Kinder lernen die Aufgaben so oder so. Aber gerade die
Kinder, denen Mathematik schwer fällt, sind davon abhängig, wie man ihnen die Inhalte aufbereitet.
Für diejenigen, die mehr dazu wissen möchten: Diesen Ansatz habe ich aus dem sehr guten Buch Einmaleins
verstehen, vernetzen, merken: Strategien gegen Lernschwierigkeiten* von Michael Gaidoschik.
Grundvorstellungen aufbauen
Tauschgesetz

Das Tauschgesetz kann, zusätzlich zu den Arbeitsblättern, ganz einfach mit einem Hunderterfeld* und ein oder zwei transparenten Folien* geübt werden.
In der ersten Variante (oberes Bild) decken Sie Felder ab. Die Frage: Welche Malaufgaben siehst du bei den offenen Feldern? Auf dem oberen Bild sehen wir z.B. die Aufgaben 6 ∙ 7 und 7 ∙ 6. In dieser Variante lassen sich Zusammenhänge gut darstellen. Man kann auf dem oberen Bild z.B. erkennen, wie viele Spalten unter der gelben Folie noch fehlen, bis man bei 10 ∙ 6 ankommt.
In der zweiten Variante (unteres Bild) geht man genau anders herum vor: Welche Malaufgaben siehst du unter der Folie? Im Beispiel wären das die Aufgaben 3 ∙ 6 und 6 ∙ 3.
Die Rollen können auch getauscht werden. Man kann z.B. dem Kind sagen: "Zeige mir die Aufgabe 5 ∙ 9." Das Kind
soll die Folien dann so legen, dass die Aufgabe zu erkennen ist.
Wer sich ein Hunderterfeld ausdrucken möchte, kann das hier tun.
Kernaufgaben
Malaufgaben ableiten
Malaufgaben gemischt
Wenn Sie nach weiterführenden Materialien suchen: Ich habe gerade in Klasse 1/2 sehr gute Erfahrungen mit den LÜK-Kästen gemacht. Die Kinder üben damit sehr gern und sehen Anhand der Muster des LÜK-Kastens ob sie richtig gerechnet haben. Wer also nach weiteren Übungsmaterialien sucht, findet hier einen LÜK-Kasten* und hier ein passendes Übungsheft* für das Einmaleins.
Die mit * gekennzeichneten Links sind sogenannte Affiliate-Links. Wenn du auf einen dieser Links klickst und ein Produkt kaufst, bekomme ich von Amazon eine Vermittlerprovision. Der Preis bleibt für dich dabei der gleiche. Dieses System hilft mir, meinen Kanal zu finanzieren und meine Videos und Arbeitsblätter weiterhin kostenlos zu halten. So haben wir beide etwas davon. :)
